Neutron Interactions

In nuclear fission reactors, neutrons cause the fission. When a neutron hits the fuel nucleus, say, U-235, the neutron is absorbed and an isotope, U-236 is formed. The U-236 is invariably in its excited state and has to de-excite. As said earlier, one possibility of de-excitation is fission, and the entire reactor programme depends on this possibility. Let us see the types of interactions that are possible, and how these are quantified. A nuclear reaction is generally symbolised as

Target (projectile, ejectile) Residue.

It indicates that a particle (projectile, say neutron) hits a nucleus (Target, say U-235), and the interaction results in a nucleus (Residue, say U-236), and a particle (ejectile, say g).

Examples:

U-235 (n,g) U-236: Capture of a neutron and ejection of g.

U-235 (n,f) Fission Products: Neutron fission

Fe-56 (n,n) Fe-56:  Scattering of a neutron.

Many types of reactions are possible when a neutron hits a nucleus. The probability of each type of reaction happening depends on the nucleus and is very sensitive to the energy of the neutron. In this regard, two neighbouring nuclides (say, of masses A and A+1) may differ drastically. Some of the prominent reactions are explained below:

Elastic scattering: The neutron and the nuclide collide and share a part of their kinetic energies. They rebound with speeds different from the original speeds, such that the ‘total kinetic energy’ before and after the collision remains the same. If the nucleus is stationary before collision, it will gain energy from the neutron and start moving, and the neutron gets slowed down due to loss of kinetic energy. However, the residual nucleus is not excited but is in its ground state.

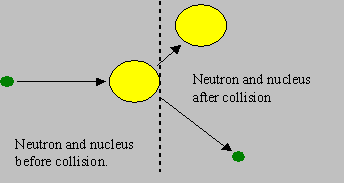
This is the type of reaction that mostly helps fast neutrons to be slowed down to low energies in a reactor. Can the neutron gain energy? Yes. However, this is obviously possible when the nucleus has higher kinetic energy than the neutron.

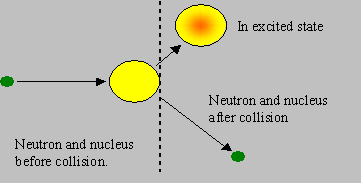
Inelastic scattering: The neutron and the nuclide collide and rebound with speeds different from the original speeds, but the rebounding nuclide is left in an excited energy state. Hence the ‘total kinetic energy’ after the collision is less than that before the collision, and this difference accounts for the energy of excitation. If the nucleus is stationary before collision, the neutron must have kinetic energy exceeding the excitation energy, so that such a reaction is possible. Hence inelastic scattering is said to be a ‘threshold reaction’, the threshold being the minimum kinetic energy of the neutron required for the reaction to be possible. The excited nucleus subsequently de-excites by emitting g radiation. Heavy nuclides have lower thresholds than light nuclides. Though the probability of inelastic scattering is generally lower than elastic, the energy loss to the neutron is higher in an inelastic collision. Inelastic scattering in heavy nuclides degrades fission neutron energies heavily.

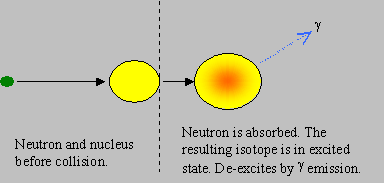
Capture: The neutron is absorbed by the target nucleus to form the next higher isotope (of mass A+1), in an excited state of energy. The new isotope de-excites by emitting g rays. The neutron is thus lost in this reaction. This is often known as ‘radiative capture’.

 (n,x) reaction: In this reaction, ‘n’ represents neutron, and ‘x’ represents any particle like neutron, proton, deutron, a particle, etc. or a combination of such particles. It means that a neutron interaction with a nuclide results in emission of the particle(s) represented by ‘x’. (e.g.) if the emitted particle is a, it is called (n,a) reaction. If a neutron and a proton are emitted, then it is called (n,np) reaction. If 2 neutrons are emitted, it is then (n,2n) reaction. Such reactions are generally threshold reactions.

Fission: This is the most important reaction upon which the present day nuclear energy programme depends. Nuclear fission is a phenomenon in which a heavy nucleus, splits into two smaller nuclei, called the fission fragments, mostly of unequal masses, one often with nearly half the mass as the other, and rarely of equal masses. This reaction gives off a large amount of energy and emits two or more neutrons, and gamma rays. When a neutron hits a heavy nuclide like U-235, the neutron gets absorbed in the heavy nuclide that gets energetically agitated (or excited). If the new energy state of the heavy nuclide is sufficient for it to split, then it can split to cause fission.  The neutrons produced in fission are fast, with an average energy of 2 MeV.

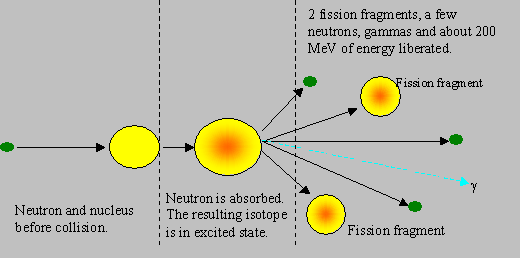
It must be noted that the fission fragments themselves are in excited state, and they de-excite generally by b, g and neutron emissions. The neutron emitted during fission are called prompt neutrons, and those emitted by the fragments after a delay are called delayed neutrons. Similary, prompt and delayed gammas are also emitted. About 80 % of the energy released in fission is carried away by the fission products (and the rest by the other particles), which in turn transfer the energy to the surroundings, making the energy recoverable. Some energy is carried away by particles known as neutrinos, which are chargeless and light, do not interact with any material, and hence their energy is not recoverable. The approximate distribution of fission energy through various emissions is given below:

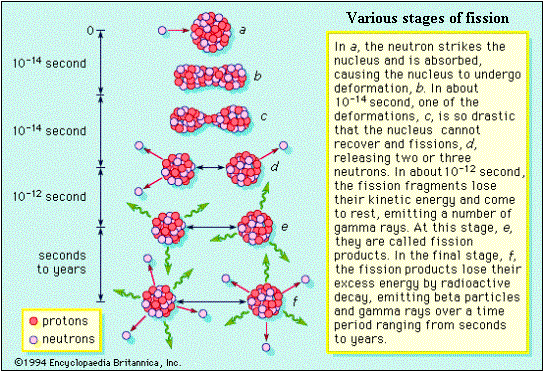
As a fission caused by a neutron involves production of further neutrons, a fission chain reaction becomes possible, and such a chain is ensured in the design of a reactor. The nuclear energy released in fission is about a million times the chemical energy released in burning a block of coal of equal mass. The following figures show the different stages in fission.

Probabilities of various reactions: A neutron-nuclear collision may result in a variety of reactions. As explained earlier, a neutron-nuclear collision could give rise to elastic or inelastic scattering, fission, or capture. A quantity called the microscopic cross-section is defined to represent the measure of the probabilities of each such reaction. It is given by the symbol s, and the reaction is indicated by a subscript in the symbol. Thus s_el refers to elastic scattering, s_in to inelastic scattering, s_f to fission, s_g  (or s_(n,g)) to radiative capture probabilities and so on. The symbol s_t called the ‘total cross-section’ is the sum of all the partial cross-sections.

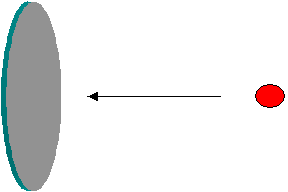
The term ‘cross-section’ generally refers to a plane surface or area of a cut-out section. The basic meaning of cross-section remains the same in the nuclear jargons as well, though it is used to represent the probability of an interaction. Imagine a projectile approaching a target as in the figure below. Obviously the chance (probability) of a collision depends on the surface area projected by the target. i.e. The probability of collision is larger if the area is larger. If there are a large number of projectiles, the number of projectiles that could hit the surface is larger if the surface area is larger. Arguing in this manner, it is easy to visualize that the probability of collision (i.e. interaction) between the target and the projectile could be expressed by the effective surface area available for the collision.

The idea is extended to represent probabilities of nuclear interactions, but a precise definition consistent with physics is employed. As the boundaries of sub-atomic systems are not sharp, the surface area supposed to be presented by a target can be larger than its geometric surface area. Thus it is now clear, in the nuclear jargons, that the term cross-section represents a measure of the ‘probability of interaction between a projectile and a target’. This quantity is usually called ‘microscopic cross-section’, represented by the symbol ‘s’, and is expressed in area units. The practical unit of microscopic cross-section is a ‘barn’, where 1 barn = 10^-24 cm² (i.e 10^-28 m²).

The neutron-nuclear microscopic cross-sections vary significantly from nuclide to nuclide and drastically with respect to neutron energy. Knowledge of cross-sections is essential to understand the physics behind the design of a nuclear reactor and also to select the composition for reactor materials. Properly averaged cross-sections are usually used. The table below gives representative (average) values of microscopic cross-sections for various materials of importance to thermal and fast reactors.

Cross-sections of some important reactor materials

Fission chain reaction: As indicated earlier, the availability of neutrons from fission helps continue the chain of fission reactions. Since more than one neutron is generated in fission, it is possible to achieve the fission chain reaction, even after accounting for other reactions of neutron, like absorption. Thus one neutron must be effectively available, after every fission for continuing the chain. The rate of production of fission neutrons depend on the cross-sections, and the composition of the fissioning material. It can be seen from the cross-section table that the cross-sections are higher when the neutron is slow than when they are fast. We must appropriately choose the fuel composition and neutron energy region to work with, to achieve the chain reaction.

Radioactivity

Index

Thermal Reactors