Thermal Reactors & Moderation

The neutrons at birth in fission are very fast with an average kinetic energy of about 2 MeV.  Let us look at the pertinent neutron-nuclear reaction properties.  A reactor works mainly based on fission chain reaction. Assume that every fission gives one neutron to continue the chain, the excess if any being lost somehow. Let s denote probability of a neutron reaction with one nuclide, with a suffix indicating the reaction, and the superscript indicating the nuclide. Let us analyze s_fU-235/s_cU-238 curve vs. energy given in the figure below. For the fissions to be more than captures, N(U-235) s_f(U-235)/N(U-238)sc(U-238) must well exceed unity. N represents the isotopic concentration. In the case of natural uranium N(U-235)/N(U-238) is about 0.7/99.3 (~0.00705) and so s_f(U-235)/s_c(U-238) must be more than 142. This condition is satisfied only in the ‘slow region’ leading to the concept of slow or thermal reactors. In the ‘fast region’, say at 100 keV, sfU-235/scU-238 is seen to be about 10, and so NU-235/NU-238 must well exceed 0.1 (i.e. 10%). It must be borne in mind that enrichment is an expensive proposition, and also would lead to faster depletion of the natural fissile viz. U-235.  Slowing down or thermalisation of neutrons permits a workable reactor with natural uranium fuel. Thermal neutrons are those that have been slowed down enough to be in thermal equilibrium with the surrounding.

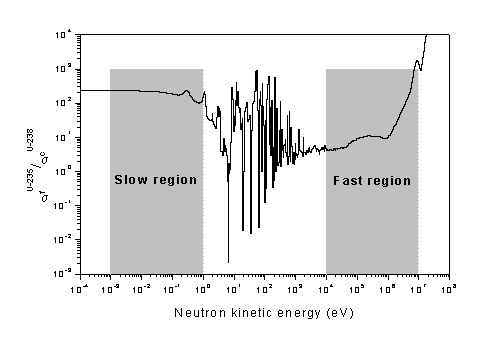
As the neutrons are fast at birth, in order to have thermal reactors, the neutrons have to be slowed down, ie. moderated. This is achieved by introducing moderators in the reactor. Moderators are generally light elements, like hydrogen, carbon (graphite), etc., that degrade the neutron energy effectively in elastic scattering collisions, mentioned earlier. As the neutron availability for chain reaction is crucial, the moderator must be chosen such that its absorption cross-section is low, but scattering cross-section is high.

It is not possible to have a fast reactor working with natural uranium fuel. The fission to capture ratio shown in the figure above looks high enough, at very high energies, to suggest that a fast reactor is feasible with natural uranium. This view may be supported by the fact that the ratio is slightly higher in the MeV range, because of U-238 fissions. However, it must be noted that most of the fission neutrons have energies just above 1 MeV where the fission to capture ratio is seen to be inadequate. It must also be noted that scattering reactions, especially the inelastic scattering, (in fuel as well as in structural materials) dominate over fissions in this region, causing the high energy neutrons to degrade to energies down below 1 MeV. For a commercial fast reactor, most of the neutrons would be populated around 100 keV. The curve in the above figure shows that a chain reaction and hence a reactor with neutrons in the fast region is not feasible, because the fissions in such a system would be far less than captures. However a working fast reactor is feasible with sufficient enrichment in the fissile content.

Figure below gives cross-sections (probabilities) for different reactions in uranium at high energies. It shows how scattering reactions dominate in the MeV range.

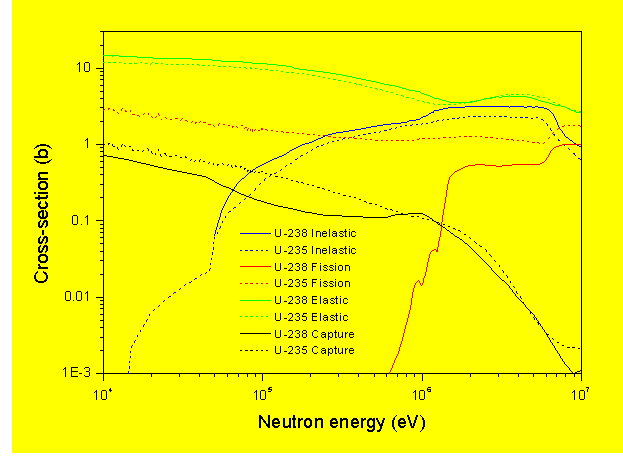
Neutron Cross-sections of U-235 and U-238 at high energies

For heavy nuclides, the energy loss in an elastic collision is much smaller than in an inelastic collision. As said earlier, elastic collision results in kinetic energy sharing. A neutron, in an elastic collision with a heavy nucleus, rebounds almost with its initial energy giving very little energy to the nucleus. But, in an inelastic collision a substantial part of neutron energy is used in leaving the nucleus in an excited state. It must be recalled that the inelastic scattering itself is possible only beyond the relevant threshold energy.

Neutron Slowing Down: As a neutron produced in fission has an average energy of 2 MeV, it has to be slowed down to thermal (0.025 eV) energies to take advantage of high fission cross-sections in the fissile (U-235) nucleus. Study of slowing down properties help selection of proper material (moderator) for the purpose. The following are obtained from the kinematics of elastic scattering collision:

If E₁ is the initial neutron energy (before collision), and E_2, its energy after collision, the maximum value of E₂ =  E₁ (glancing collision) and the minimum value of E₂ = aE₁ (head-on collision), where a = [(A-1)/(A+1)]². This gives the maximum energy loss in a collision at E₁ is (1-a)E_1.  The average average loss is given by (1-a)E₁/2.

The average cosine of the scattering angle (in the Laboratory system of coordinates), <cosy> = 2/3A, where A is nuclear mass in terms of neutron mass. For high A,  <cosy> approaches zero, indicating a tendency to isotropy (i.e. all angles are equally probable).

The logarithmic energy decrement is given by log(E₁ / E₂). The average value of this quantity, per collision is given by x = 2/(A+2/3), which is independent of initial neutron energy. This indicates that, in every elastic collision, on an average, the neutron energy decrement is by a constant ratio, irrespective of its initial energy. From this, the number of collisions needed to bring a neutron from an initial energy E₀ to a given energy E, is given by (1/x)ln(E₀ / E). Thus the number of collisions required to slow down a 2 MeV neutron to 0.025 eV is given by ln(2´10⁶/0.025) / x.

If E₀ is an arbitrary high energy, the logarithmic decrement to a given energy E is ln(E₀/E). Keeping the E₀ as the reference (initial) energy, a quantity Lethargy can be defined as u = ln(E₀/E). As E decreases u increases. Taking differentials, du = -dE/E. du represents infinitesimal log energy decrement.

For a good moderator high x, high scattering cross-section and low absorption cross-section are preferred, for obvious reasons.  xS_s is known as Slowing-down Power; and xS_s /S_a is called the Moderating Ratio (MR). A material with high MR is preferable.  The slowing down parameters of various nuclei are given below:

Neutron Interactions

Index

Breeder Reactor