Nuclear physics is a vast branch of physics. It deals with the properties of an atomic nucleus, such as mass, charge, size, nucleons (neutrons and protons) and their binding energies, nuclear structure, bound and excited energy levels, spin states, interaction behaviour with gamma rays, with other particles, and with other nuclei, variation of such behaviour with energy and angle of interaction, the nuclear stability, radioactivity of excited and unexcited nucleus, decay half-lives, decay particles and their energies, nuclear transmutations, and so on. The aim of the subject is to understand the properties of the nuclei, both quantitatively and qualitatively. A variety of highly sophisticated nuclear physics experiments aid such an understanding. A detailed understanding needs quantum mechanical interpretations and advanced mathematics. A thorough understanding will facilitate exploitation of nuclear properties for the benefit of mankind. We present below some basic notions of nuclear physics, that help us appreciate the principles and mechanisms of nuclear-energy production.
It has been amply understood that substantial nuclear energy is released in breaking a heavy nucleus into lighter ones (known as fission) and in joining lighter nuclei together to form a heavier one (known as fusion). Which heavy nucleus to break? How to break it? Which light nuclei to fuse? How to fuse them? What are the arrangements and precautions needed? How to extract the energy released and make it available for human use? Is nuclear energy production economical, practicable and safe? Are there different options available? Such and many more questions arise. All such questions have to be answered satisfactorily before venturing into projects in nuclear energy production. However, the fundamental mechanism of nuclear energy production can be appreciated by going through the basic nuclear physics aspects that follow:
AN ATOMIC NUCLEUS
An atom consists of a centrally located nucleus surrounded by electrons revolving in certain physically permitted orbits. The nucleus itself is made up of neutrons and protons, collectively called nucleons.

The neutrons are electrically neutral, the protons positive (with 1.6 x 10-19 coulomb of charge) and the electrons negative with the same magnitude of charge. The nuclear dimension is in the range of 10-13 – 10-12 cm, while the atomic dimension is about 10-8 cm. That is, the diameter of an atom is over 10,000 times the diameter of its nucleus. 1 cm is nearly the width of our little finger. The atomic diameter is about one hundred millionth the width of our little finger. The nuclear size is 1 billionth the width of our little finger. This nuclear range is called a short-range, wherein the nucleons attract each other with a force, much larger than the electrostatic repulsion between the positively charged protons. This means, two neutrons attract each other though they are neutral; two protons attract each other though they are both positively charged; a proton and a neutron attract each other though they are not of opposite charges. In other words the nucleons bind themselves together when they happen to come closer than 10-12 cm. Within this range, the closer they are the stronger their bond is.
The electron orbit need not be circular, but may be oval in shape. Generally, there are as many electrons around the nucleus as there are protons in the nucleus, thus making the atom as a whole, neutral. Please note that the atomic neutrality is with respect to a point sufficiently away from the atom, since the influences of electrons and protons cancel out. The respective charge would be felt, very close to the electron or the nucleus. If one or more electrons are removed from the orbit, the atom has a net positive charge, and is said to be positively ionized. Similarly, if electrons are added to the orbits, the atom becomes negatively ionized. See figure below:
|
Neutral atom |
Positively ionized atom |
Negatively ionized atom |
|
|
|
|
|
|
||
The number of protons (Z) is called the atomic number and the total number (A) of nucleons in a nucleus is called the atomic (or nuclear) mass number. Occasionally the number of neutrons (A-Z) is represented as N. Atoms are classified as isotopes, isotones, and isobars based on the nuclear contents, as below:
|
Isotopes |
Isotones |
Isobars |
|
Nuclei with same Z but differing in N |
Nuclei with same N but differing in Z |
Nuclei with same A but differing in N, Z or both |
|
Example: U-235, U-238 |
Example: U-238, Np-239 |
Example: U-238, Np-238, Pu-238 |
There are about 266 stable nuclides, and 65 radioactive nuclides in nature. A radioactive nucleus is one in an unstable configuration. It approaches stable configuration(s), by emitting radiation in the form of gamma energy, or particles like alpha, beta, neutron, etc., or by splitting into fragments. The internal energy state of a nucleus is responsible for the stability of a nucleus, and is affected by the number of protons and number of neutrons in the nucleus. The following table gives the distribution of the stable nuclei with respect to even/odd combinations of Z and N. It shows that an even-even combination of Z and N gives high stability, and odd-odd the least.
Stable nuclides
|
A |
Z |
N |
Number |
|
Even |
Even |
Even |
159 |
|
Odd |
Even |
Odd |
53 |
|
Odd |
Odd |
Even |
50 |
|
Even |
Odd |
Odd |
4 |
|
Total |
266 |
||
Further, Z or N = 2,8,20,50,82,126 gives high stability to a nucleus, and these numbers are referred to as magic numbers. If Z and N of a nucleus happen to be individually equal to magic numbers, the configuration is called doubly magic leading to exceptional stability. The magic numbers are not mythical, though they appear to be so. A nucleus is understood to be formed in a shell-structure, with each shell having a ‘capacity’ for filling with neutrons or protons. Each shell gets ‘closed’ when it is filled to full capacity. Quantum mechanical arguments show that the capacities of different shells correspond to the (so called) magic numbers. If all the shells of a nucleus are closed, it becomes very stable.
As said, the stability of a nucleus is influenced by the numbers of protons and neutrons in it. Hydrogen 1H1 has one proton and no neutron. This is the only nucleus without a neutron. An isotope of hydrogen, viz. heavy hydrogen 2H1, some times called ‘deuterium 2D1’, has a proton and a neutron. Light stable nuclei, except 1H1, have generally equal number of protons and neutrons. As the nucleus becomes heavier, the N/Z ratio, or the ‘neutron-to-proton ratio’ of stable nuclides increases. As said earlier, the nuclear short-range attractive force is the same between any type of nucleons. As the number of protons increases, the electric repulsive force becomes more and more significant. Neutrons have no electric repulsion but only attraction. Hence adequate presence of neutrons will help overcome the average repulsive force per nucleon in the nucleus. Thus stability of a high-Z nucleus demands that the number of neutrons well exceeds the number of protons. In other words, more neutrons than protons are needed to support the binding of the positively charged protons within the nucleus, as the proton number gets larger. One must not jump to the conclusion that the more the neutrons, the more stable the nucleus is. The picture below shows the numbers of neutrons and protons in stable nuclei and illustrates how the N/Z ratio deviates from unity. The black squares indicating stable nuclides form an approximate line called the ‘Stability Line’. Sometimes it is called the ‘beta stability line’.
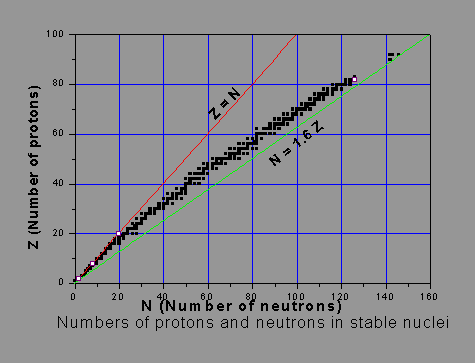
Excessive or inadequate number of neutrons, as compared to the stability-line, leads to instability of the nucleus, leading to its radioactivity. Some of the very stable (magic) nuclei (e.g. lead, with 82 protons and 126 neutrons), are shown as open squares.
The masses of sub-atomic particles are often expressed in ‘atomic mass unit (amu)’.
1 amu = 1.6606 x 10-27 kg. The masses of proton, neutron and electron are given below:
|
Particle |
Mass (amu) |
|
Proton |
1.007277 |
|
Neutron |
1.008665 |
|
Electron |
0.0005486 |
This shows that a neutron is slightly heavier than a proton, and an electron is lighter by a factor of about 1840.
According to Einstein, energy and mass are related. Energy = mass ´ c2, where c is the speed of light = 2.998 ´ 108 m/s. The unit of energy often chosen in nuclear physics is an electron-volt (eV). 1 eV is the energy associated with an electron moving across a potential difference of 1 Volt. 1 million eV is denoted as MeV. 1 MeV = 1.602 x 10-13 Joules. 1 amu = 931.5 MeV. These units will be extensively used in discussions below.
Binding Energy: The nuclear source of energy is understood only if the concept of binding energy (BE) is understood. The nucleons, as said, are held by short-range nuclear forces. The mass of a nucleus is generally less than the sum of the masses of the nucleons. This difference is called the mass-defect. Such a phenomenon is observed in atomic or subatomic levels, and not with ordinary materials that we handle, where the total mass has to be the sum of the component masses. The mass-defect is responsible for the binding together of the nucleons. The energy equivalent of the mass-defect is called the binding-energy of the nucleus. Look at the following illustrative picture and visualize that, when individual nucleons pack themselves together to form a system, which we call nucleus, they liberate some energy in the form of photons (gamma rays). The liberated energy manifests as a reduction in the net mass of the nucleus, as per Einstein’s relation. It may also be said that the nucleus could be split into nucleons by supplying external energy equal to the binding energy.
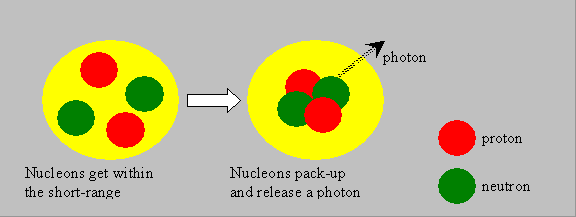
|
Example: For the He-4 nucleus, the binding energy may be computed as below: Total mass of 2 protons = 2 ´ 1.00728 = 2.01456 amu Total mass of 2 neutrons = 2 ´ 1.00866 = 2.01732 amu Total mass of nucleons = 4.03188 amu Mass of Alpha particle (measured) = 4.00153 amu Mass defect Dm = 0.03035 amu Hence, Binding energy of He-4 = 28.3 MeV. ( i.e. 0.03035 amu ´ 931.5 MeV/amu)
|
The enormity of the nuclear binding energy can be better appreciated by comparing it to the binding energy of an electron in an atom. The nuclear binding energies are on the order of a million times greater than the electron binding energies of atoms. For example, the binding energy of an electron to the nucleus in the hydrogen atom is 13.6 eV, whereas the binding energy of nucleons in the He-4 nucleus is 28,300,000 eV (roughly 2 million times!)
Binding Energy Per Nucleon (BE/A): As the number of particles in a nucleus increases, the total binding energy also increases. The rate of increase, however, is not uniform. This lack of uniformity results in a variation in the amount of binding energy associated with each nucleon within the nucleus. This variation in the binding energy per nucleon (BE/A) is easily seen when the average BE/A is plotted versus atomic mass number (A), as shown in the figure below:
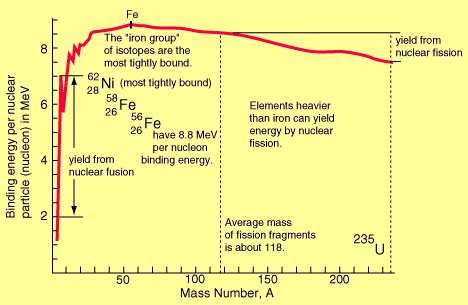
Binding Energy per Nucleon vs. Mass Number
The above figure illustrates that as the atomic mass number increases, the binding energy per nucleon decreases for A > 60. The BE/A curve reaches a maximum value of 8.79 MeV at A = 56 and decreases to about 7.6 MeV for A = 238.
The general shape of the BE/A curve can be explained using the general properties of nuclear forces. As already said, very short-range attractive forces that exist between nucleons hold the nucleus in its shape. On the other hand, the long-range repulsive electrostatic (coulomb) forces that exist between all the protons in the nucleus continuously tend to force the protons apart, thus splitting the nucleus. As the atomic number (Z) increases, the repulsive electrostatic forces within the nucleus increase. To overcome this increased repulsion and maintain stability, the proportion of neutrons in the nucleus must increase. This increase in the neutron-to-proton ratio only partially compensates for the growing proton-proton repulsive force in the heavier, naturally occurring elements. As the repulsive forces are increasing, less energy must be supplied, on the average, to remove a nucleon from the nucleus. In other words, the BE/A has decreased. The BE/A of a nucleus is an indication of its degree of stability. Generally, the more stable nuclides have higher BE/A than the less stable ones. The increase in the BE/A as the atomic mass number decreases from 260 to 60 is the primary reason for the energy liberation in the fission process. In addition, the increase in the BE/A as the atomic mass number increases from 1 to 60 is the reason for the energy liberation in the fusion process, which is the opposite reaction of fission.
The heaviest nuclei require only a small energy addition for the relatively large coulomb forces to overcome the attractive nuclear forces, in order to split the nucleus into two halves. Consequently, the heaviest nuclei are easily fissionable compared to lighter nuclei. The addition of the energy required to cause a distortion in the heavy nucleus leading to fission, is commonly achieved by adding a neutron into the nucleus. Some nuclei experience chances of undergoing fission, even without adding a neutron, such a phenomenon being called ‘Spontaneous fission’.
In the fusion of Deuterium (a hydrogen isotope H-2) and Tritium (another hydrogen isotope H-3), called the D-T fusion, the total energy released is 17.6 MeV. In the fission of U-235 by neutron, the energy released is about 200 MeV. Though fission energy seems higher, the release of energy per unit mass of the fuel, is much higher in the case of fusion than in fission. More discussion on fission and fusion follows in the later part.
Radioactivity: Atomic nuclei that are not stable, tend to approach stable configuration(s), by the process of radioactivity. Atoms are radioactive because the ratio of neutrons to protons is not ideal. Through radioactive decay, the nucleus approaches a more stable neutron to proton ratio. Radioactive decay releases different types of energetic emissions. The three most common types of radioactive emissions are alpha particles, beta particles, and gamma rays. Fission is also a form of radioactive decay.
Alpha (a) decay occurs when the neutron to proton ratio is too low. Alpha decay emits an alpha particle, which consists of two protons and two neutrons. This is the same as a helium nucleus and often uses the same chemical symbol 4He2. Alpha particles are highly ionizing (e.g. deposits energy over a short distance). Since alpha particles lose energy over a short distance, they cannot travel far in most of the medium. For example, the range of a 5 MeV alpha particle in air is only 3.5 cm. Consequently, alpha particles will not normally penetrate the outermost layer of the skin. Therefore, alpha particles pose little external radiation field hazard. Shielding of alpha particles is easily accomplished with minimal amounts of shielding. Examples of alpha particle emitting radio-nuclides include 238U, 239Pu, and 241Am.
238U92 à 234Th90 + 4He2.
239Pu94 à 235U92 + 4He2.
241Am95 à 237Np93 + 4He2.
After the emission of an a particle, the daughter product remaining, will be reduced by 4 in its mass number, and 2 in its atomic number, as could be verified in the examples above.

Beta (b-) decay occurs when the neutron to proton ratio is too high. The radioactive nucleus emits a beta particle, which is essentially an electron, in order to bring this to a more favourable ratio. Beta particles are less ionizing than alpha particles. The range of beta particles depends on the energy, and some have enough to be of concern regarding external exposure. A 1 MeV beta particle can travel approximately 12 feet in air. Energetic beta particles can penetrate into the body and deposit dose to internal structures near the surface. Since beta particles are less ionizing than alpha particles, greater shielding is required. Low Z materials are selected as beta particle shields to take care of X-ray emissions associated with slowing down of beta particles while they travel in a medium.
In b emission, the neutron to proton ratio is reduced by converting a neutron into proton as:
1n0 à 1p1 + e-. The electron ejected is the b particle that is released. Thus b emission results in the increase of the proton number, i.e. Z, by 1, but the mass number A is unaltered. Example of b decay: 40K19 à 40Ca20 + β-1

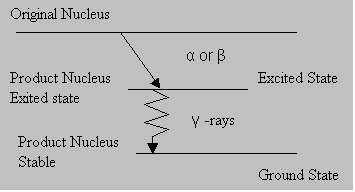
Gamma (g) rays are not particulate radiation like the alpha and beta, but a form of high-energy electromagnetic wave. Gamma rays are the least ionizing of the three forms discussed. An 1 MeV gamma ray can travel at an average of 130 meters in air. Since gamma radiation can travel far in air, it poses a significant external radiation hazard. Further, if ingested, it may pose an internal radiation hazard. Shielding of gamma rays is normally accomplished with high atomic number materials such as lead. [Gamma rays are electro-magnetic radiations with energies higher than X-rays. X-rays are produced when electrons of an atom jump from one orbital location to another. The gamma rays are released when an atomic nucleus releases its excess energy. It is clear from this that nuclear transitions involve much larger energies than the atomic transitions. In other words, energies of nuclear origin are many (103 – 106) times greater than the energies of atomic origin].
Emission of γ-rays doesn’t change the Mass number nor Atomic number. If an atom is in exited state it comes to stable state by emitting a γ radiation.
|
|
|
Usually after α or β decay, the product nucleus is formed in an excited state and it reaches a stable state after γ emission.
|
|
There are several other particles, like neutron, proton, 3He, deuterium, etc. that may be liberated in radioactivity. When a nucleus emits such particle(s) toward reaching a stable configuration, it is said to ‘decay’. The emitted particle is associated with the ‘mode’ of decay. Thus we have alpha decay, beta-decay, gamma decay, neutron-decay, etc. In the case of gamma emission, the nucleus changes only in its energy state. By particle emission, the nucleus changes into another, and so is said to be transmuted or converted. Thus there is a reduction in the original quantity of the substance, during decay. There is no fixed time between two consecutive emissions, but on an average, radioactive decay of a substance takes place at a rate, which is proportional to the number of atoms present, at a given time. This is expressed in a well-known differential equation, called radioactivity decay equation.
An atom becomes radioactive if its nucleus suffers instability, as said earlier. A nucleus may be radioactive due to instability set in while it was formed in nature. This is called ‘natural radioactivity’, like that of 238U. When a nucleus is ‘disturbed or excited’, say, by bombarding it with a particle or gamma rays, its state of stability is altered and the altered system will become radioactive. This is referred to as ‘induced radioactivity’ or ‘artificial radioactivity’. There could be many ways of putting a nucleus in a slightly or heavily unstable or ‘excited’ state. But the consequent radioactivity, which is a process of de-excitation, is governed by common laws. The de-excitation may take place quickly (say, in micro-seconds) or over a long period (in millions of years), in a single step or in a series of many steps. Hence when we talk of the radioactivity of a substance, we talk of the original radioactive material (parent), what fraction of it gets converted in unit time, what are the particles released (emitted), how much energy is released, what are the new materials (daughter products) formed, radioactivity features of the daughter products, and of the end-product (stable) as well. The rate at which the decay takes place is called ‘activity’.
Rate of Radioactive Decay: The nuclei of a given radioactive species have a definite probability of decaying in unit time; this decay probability has a constant value characteristic of the particular nuclide. It remains the same irrespective of the chemical or physical state of the element at all readily accessible temperatures and pressures. In a given specimen the rate of decay at any instant is always directly proportional to the number of radioactive atoms of the nuclide under consideration present at that instant. Thus, if N is the number of the particular radioactive atoms (or nuclei) present at any time t, the decay rate is given by
dN/dt = -λt
where λ, called the decay constant of the radioactive nuclide, is a measure of its decay probability in unit time. Upon integration between any arbitrary zero time, when the number of radioactive nuclei of the specified kind present is N0, and a time t later, when N of these nuclei remain, radioactive decay is seen to be an exponential process, the actual decay rate being determined by the decay constant λ and by the number of the particular nuclei present.
ln(N/N0) = -λt,
N=N0e-λt
Mean life: The reciprocal of the decay constant, represent by tm, is called as the mean life (or average life) of the radioactive species; thus,
tm=1/λ
The mean life is equal to the average life expectancy of the radioactive species.
Half life: It is defined as the time required for the number of radioactive nuclei of a given kind (or for their activity) to decay to half its initial value. Because of the exponential nature of the decay, this time is independent of the amount of the radionuclide present. It can be seen from the equations given above, that the half life is given by
t1/2=(ln 2)/λ = 0.6931/λ
or
t1/2=0.6931tm
The half life is thus inversely proportional to decay constant and directly proportional to mean life. The half-lives of known radioactive nuclides range from a small fraction, e.g., about a millionth of a second to billions of years.
Units to express radioactivity emission: There are several different units used to describe radiation and its effects. The simplest unit is that of activity which is measured in number of disintegrations per second (dps). One dps means a radioactive nucleus gives off one particle or photon in one second. This unit, in the international system of units (SI) system, is called the becquerel (Bq), which is equivalent to 1 dps. The other unit prevalent for the activity, is a Curie (Ci). 1 Ci = 3.7 ´ 1010 Bq. These units do not distinguish between alpha, beta or even gamma. These units provide an understanding of the "strength" of the radioactive sample but do not account for any of the properties of the radiation emitted. To describe the degree of hazard to people from a particular radiation requires other units.
Energy Levels: As mentioned earlier, ‘quantum mechanics’ is needed to understand and quantify atomic and subatomic features. The Quantum Theory recognizes restrictions in the levels of energy acquired by a system. The electrons in their orbits, or the nucleons in the shells are filled following such restrictions. The energy of an electron depends on its orbit, and only certain orbits are permitted by nature. Similarly the nucleons within a nucleus occupy different energy states that are permitted. We understand from this that an electron or a nucleon cannot go to any arbitrary energy level. Thus when the system is specified, the allowed energy states get specified. These are known as discrete energy levels. Transition from one such level to the next lower level will involve release of energy that is exactly the difference between these two levels, and cannot be a fraction of the same. The energy is said to get ‘quantised’. The electron orbits permitted for an atom are characteristic of that (species of) atom, and when an electron jumps from one orbit to the lower one, X-ray, called ‘characteristic X-ray’, with energy equal to the difference between the energies associated with the two orbits emerges. This helps even identifying the atom from which the X-rays ejected. Similar nature applies to nuclei too. Though there are no orbits inside a nucleus for the nucleons to move around, they have their energy states. A given radioactive gamma-emitting nucleus will eject gamma rays (called gamma quanta) characteristic of the nucleus. The energies taken by the nucleons within an unexcited nucleus are called bound levels.
Similarly, a nucleus could be raised (excited) in its internal energy only to certain permitted levels. These levels are called excited levels. This varies from nucleus to nucleus, but is fixed for a given nucleus. When the nucleus is unexcited, it is said to be in its ground state. The separation between two level energies decreases as the energy increases. When a nucleus is excited to a particular level, it de-excites to reach the ground state by emitting a neutron, gamma quanta, or any other particle. Fission also is such a process. The de-excitation could be in a single step, or in multiple steps involving a series of particle emissions or gamma or both.
Neutron interactions: In nuclear fission reactors, neutrons cause the fission. When a neutron hits the fuel nucleus, say, U-235, the neutron is absorbed and an isotope, U-236 is formed. The U-236 is invariably in its excited state and has to de-excite. As said earlier, one possibility of de-excitation is fission, and the entire reactor programme depends on this possibility. Let us see the types of interactions that are possible, and how these are quantified. A nuclear reaction is generally symbolised as
Target (projectile, ejectile) Residue.
It indicates that a particle (projectile, say neutron) hits a nucleus (Target, say U-235), and the interaction results in a nucleus (Residue, say U-236), and a particle (ejectile, say g).
Examples:
U-235 (n,g) U-236: Capture of a neutron and ejection of g.
U-235 (n,f) Fission Products: Neutron fission
Fe-56 (n,n) Fe-56: Scattering of a neutron.
Many types of reactions are possible when a neutron hits a nucleus. The probability of each type of reaction happening depends on the nucleus and is very sensitive to the energy of the neutron. In this regard, two neighbouring nuclides (say, of masses A and A+1) may differ drastically. Some of the prominent reactions are explained below:
Elastic scattering: The neutron and the nuclide collide and share a part of their kinetic energies. They rebound with speeds different from the original speeds, such that the ‘total kinetic energy’ before and after the collision remains the same. If the nucleus is stationary before collision, it will gain energy from the neutron and start moving, and the neutron gets slowed down due to loss of kinetic energy. However, the residual nucleus is not excited but is in its ground state.
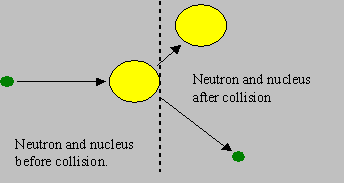
This is the type of reaction that mostly helps fast neutrons to be slowed down to low energies in a reactor. Can the neutron gain energy? Yes. However, this is obviously possible when the nucleus has higher kinetic energy than the neutron.
Inelastic scattering: The neutron and the nuclide collide and rebound with speeds different from the original speeds, but the rebounding nuclide is left in an excited energy state. Hence the ‘total kinetic energy’ after the collision is less than that before the collision, and this difference accounts for the energy of excitation. If the nucleus is stationary before collision, the neutron must have kinetic energy exceeding the excitation energy, so that such a reaction is possible. Hence inelastic scattering is said to be a ‘threshold reaction’, the threshold being the minimum kinetic energy of the neutron required for the reaction to be possible. The excited nucleus subsequently de-excites by emitting g radiation. Heavy nuclides have lower thresholds than light nuclides. Though the probability of inelastic scattering is generally lower than elastic, the energy loss to the neutron is higher in an inelastic collision. Inelastic scattering in heavy nuclides degrades fission neutron energies heavily.
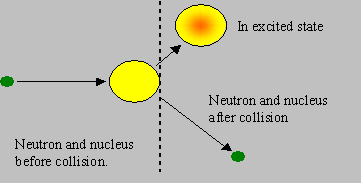
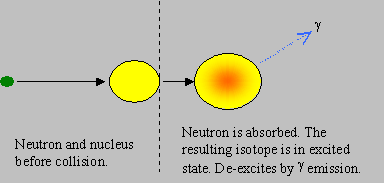
Capture: The neutron is absorbed by the target nucleus to form the next higher isotope (of mass A+1), in an excited state of energy. The new isotope de-excites by emitting g rays. The neutron is thus lost in this reaction. This is often known as ‘radiative capture’.
(n,x) reaction: In this reaction, ‘n’ represents neutron, and ‘x’ represents any particle like neutron, proton, deutron, a particle, etc. or a combination of such particles. It means that a neutron interaction with a nuclide results in emission of the particle(s) represented by ‘x’. (e.g.) if the emitted particle is a, it is called (n,a) reaction. If a neutron and a proton are emitted, then it is called (n,np) reaction. If 2 neutrons are emitted, it is then (n,2n) reaction. Such reactions are generally threshold reactions.
Fission: This is the most important reaction upon which the present day nuclear energy programme depends. Nuclear fission is a phenomenon in which a heavy nucleus, splits into two smaller nuclei, called the fission fragments, mostly of unequal masses, one often with nearly half the mass as the other, and rarely of equal masses. This reaction gives off a large amount of energy and emits two or more neutrons, and gamma rays. When a neutron hits a heavy nuclide like U-235, the neutron gets absorbed in the heavy nuclide that gets energetically agitated (or excited). If the new energy state of the heavy nuclide is sufficient for it to split, then it can split to cause fission. The neutrons produced in fission are fast, with an average energy of 2 MeV.
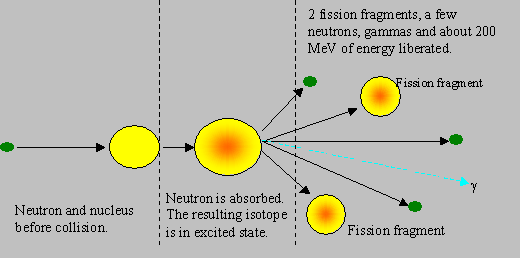
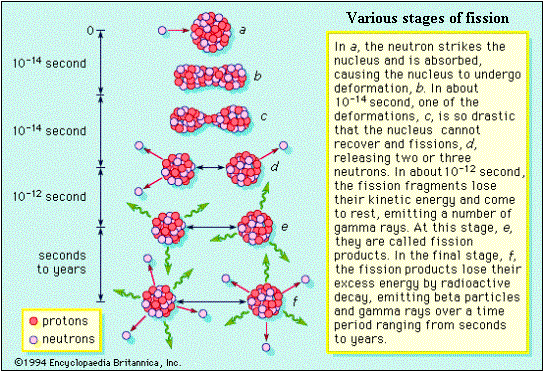
It must be noted that the fission fragments themselves are in excited state, and they de-excite generally by b, g and neutron emissions. The neutron emitted during fission are called prompt neutrons, and those emitted by the fragments after a delay are called delayed neutrons. Similary, prompt and delayed gammas are also emitted. About 80 % of the energy released in fission is carried away by the fission products (and the rest by the other particles), which in turn transfer the energy to the surroundings, making the energy recoverable. Some energy is carried away by particles known as neutrinos, which are chargeless and light, do not interact with any material, and hence their energy is not recoverable. The approximate distribution of fission energy through various emissions is given below:
|
Kinetic energy of fission fragments |
170 MeV |
|
Prompt radiations (gammas and neutrons) |
12 MeV |
|
Delayed radiations (neutrons and gammas) |
12 MeV |
|
Neutrinos (unrecoverable) |
8 MeV |
|
Total |
202 MeV |
As a fission caused by a neutron involves production of further neutrons, a fission chain reaction becomes possible, and such a chain is ensured in the design of a reactor. The nuclear energy released in fission is about a million times the chemical energy released in burning a block of coal of equal mass. The following figures show the different stages in fission.
Probabilities of various reactions: A neutron-nuclear collision may result in a variety of reactions. As explained earlier, a neutron-nuclear collision could give rise to elastic or inelastic scattering, fission, or capture. A quantity called the microscopic cross-section is defined to represent the measure of the probabilities of each such reaction. It is given by the symbol s, and the reaction is indicated by a subscript in the symbol. Thus sel refers to elastic scattering, sin to inelastic scattering, sf to fission, sg (or s(n,g)) to radiative capture probabilities and so on. The symbol st called the ‘total cross-section’ is the sum of all the partial cross-sections.
The term ‘cross-section’ generally refers to a plane surface or area of a cut-out section. The basic meaning of cross-section remains the same in the nuclear jargons as well, though it is used to represent the probability of an interaction. Imagine a projectile approaching a target as in the figure below. Obviously the chance (probability) of a collision depends on the surface area projected by the target. i.e. The probability of collision is larger if the area is larger. If there are a large number of projectiles, the number of projectiles that could hit the surface is larger if the surface area is larger. Arguing in this manner, it is easy to visualize that the probability of collision (i.e. interaction) between the target and the projectile could be expressed by the effective surface area available for the collision.
The idea is extended to represent probabilities of nuclear interactions, but a precise definition consistent with physics is employed. As the boundaries of sub-atomic systems are not sharp, the surface area supposed to be presented by a target can be larger than its geometric surface area. Thus it is now clear, in the nuclear jargons, that the term cross-section represents a measure of the ‘probability of interaction between a projectile and a target’. This quantity is usually called ‘microscopic cross-section’, represented by the symbol ‘s’, and is expressed in area units. The practical unit of microscopic cross-section is a ‘barn’, where 1 barn = 10-24 cm2 (i.e 10-28 m2).
The neutron-nuclear microscopic cross-sections vary significantly from nuclide to nuclide and drastically with respect to neutron energy. Knowledge of cross-sections is essential to understand the physics behind the design of a nuclear reactor and also to select the composition for reactor materials. Properly averaged cross-sections are usually used. The table below gives representative (average) values of microscopic cross-sections for various materials of importance to thermal and fast reactors.
Cross-sections of some important reactor materials
|
Material |
Cross-sections in barns |
||||
|
Thermal neutrons (E = 0.0253 eV) |
Fast neutrons (E > 100 eV) |
||||
|
Fission |
Capture |
Fission |
Capture |
||
|
Fissile |
92-U-233 |
528.45 |
45.76 |
2.7323 |
0.27176 |
|
92-U-235 |
585.086 |
98.6864 |
1.9041 |
0.55549 |
|
|
94-Pu-239 |
747.401 |
270.329 |
1.7973 |
0.49614 |
|
|
Fertile |
92-U-238 |
0.00001177 |
2.71692 |
0.042758 |
0.33188 |
|
90-Th-232 |
0.0 |
7.4 |
0.010193 |
0.38157 |
|
|
Clad |
40-Zr |
|
0.185396 |
|
0.0265766 |
|
Steel |
|
3.08668 |
|
0.0170228 |
|
|
Coolant |
Light Water |
|
0.664 |
|
0.00051554 |
|
Heavy Water |
|
0.0013 |
|
0.00011459 |
|
|
11-Na-23 |
|
0.528 |
|
0.0027511 |
|
|
Control Rod |
5-B-10 |
|
3840.0 |
|
2.73462 |
|
48-Cd |
|
2524.15 |
|
0.266766 |
|
|
Fission Products |
54-Xe-135 |
|
2636300.0 |
|
0.0059985 |
|
36-Kr-83 |
|
207.667 |
|
0.235944 |
|
|
62-Sm-149 |
|
40144.3 |
|
1.91883 |
|
Fission chain reaction: As indicated earlier, the availability of neutrons from fission helps continue the chain of fission reactions. Since more than one neutron is generated in fission, it is possible to achieve the fission chain reaction, even after accounting for other reactions of neutron, like absorption. Thus one neutron must be effectively available, after every fission for continuing the chain. The rate of production of fission neutrons depend on the cross-sections, and the composition of the fissioning material. It can be seen from the cross-section table that the cross-sections are higher when the neutron is slow than when they are fast. We must appropriately choose the fuel composition and neutron energy region to work with, to achieve the chain reaction.
Thermal reactors and moderation: The neutrons at birth in fission are very fast with an average kinetic energy of about 2 MeV. Let us look at the pertinent neutron-nuclear reaction properties. A reactor works mainly based on fission chain reaction. Assume that every fission gives one neutron to continue the chain, the excess if any being lost somehow. Let s denote probability of a neutron reaction with one nuclide, with a suffix indicating the reaction, and the superscript indicating the nuclide. Let us analyze sfU-235/scU-238 curve vs. energy given in the figure below. For the fissions to be more than captures, N(U-235) sf(U-235)/N(U-238)sc(U-238) must well exceed unity. N represents the isotopic concentration. In the case of natural uranium N(U-235)/N(U-238) is about 0.7/99.3 (~0.00705) and so sf(U-235)/sc(U-238) must be more than 142. This condition is satisfied only in the ‘slow region’ leading to the concept of slow or thermal reactors. In the ‘fast region’, say at 100 keV, sfU-235/scU-238 is seen to be about 10, and so NU-235/NU-238 must well exceed 0.1 (i.e. 10%). It must be borne in mind that enrichment is an expensive proposition, and also would lead to faster depletion of the natural fissile viz. U-235. Slowing down or thermalisation of neutrons permits a workable reactor with natural uranium fuel. Thermal neutrons are those that have been slowed down enough to be in thermal equilibrium with the surrounding.
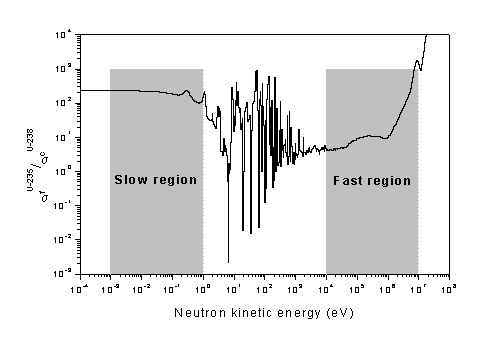
As the neutrons are fast at birth, in order to have thermal reactors, the neutrons have to be slowed down, ie. moderated. This is achieved by introducing moderators in the reactor. Moderators are generally light elements, like hydrogen, carbon (graphite), etc., that degrade the neutron energy effectively in elastic scattering collisions, mentioned earlier. As the neutron availability for chain reaction is crucial, the moderator must be chosen such that its absorption cross-section is low, but scattering cross-section is high.
It is not possible to have a fast reactor working with natural uranium fuel. The fission to capture ratio shown in the figure above looks high enough, at very high energies, to suggest that a fast reactor is feasible with natural uranium. This view may be supported by the fact that the ratio is slightly higher in the MeV range, because of U-238 fissions. However, it must be noted that most of the fission neutrons have energies just above 1 MeV where the fission to capture ratio is seen to be inadequate. It must also be noted that scattering reactions, especially the inelastic scattering, (in fuel as well as in structural materials) dominate over fissions in this region, causing the high energy neutrons to degrade to energies down below 1 MeV. For a commercial fast reactor, most of the neutrons would be populated around 100 keV. The curve in the above figure shows that a chain reaction and hence a reactor with neutrons in the fast region is not feasible, because the fissions in such a system would be far less than captures. However a working fast reactor is feasible with sufficient enrichment in the fissile content.
Figure below gives cross-sections (probabilities) for different reactions in uranium at high energies. It shows how scattering reactions dominate in the MeV range.
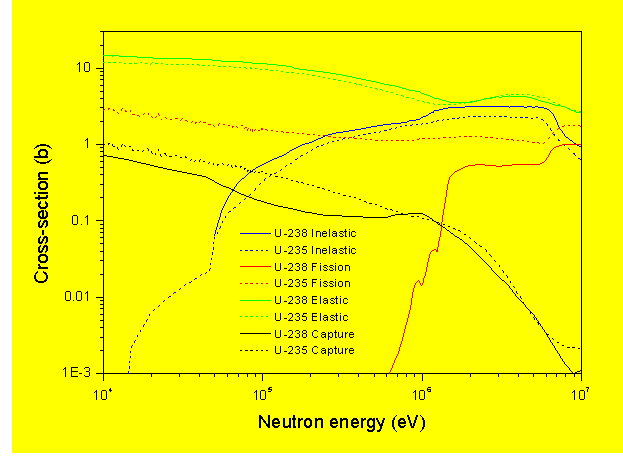
Neutron Cross-sections of U-235 and U-238 at high energies
For heavy nuclides, the energy loss in an elastic collision is much smaller than in an inelastic collision. As said earlier, elastic collision results in kinetic energy sharing. A neutron, in an elastic collision with a heavy nucleus, rebounds almost with its initial energy giving very little energy to the nucleus. But, in an inelastic collision a substantial part of neutron energy is used in leaving the nucleus in an excited state. It must be recalled that the inelastic scattering itself is possible only beyond the relevant threshold energy.
Neutron Slowing Down: As a neutron produced in fission has an average energy of 2 MeV, it has to be slowed down to thermal (0.025 eV) energies to take advantage of high fission cross-sections in the fissile (U-235) nucleus. Study of slowing down properties help selection of proper material (moderator) for the purpose. The following are obtained from the kinematics of elastic scattering collision:
If E1 is the initial neutron energy (before collision), and E2, its energy after collision, the maximum value of E2 = E1 (glancing collision) and the minimum value of E2 = aE1 (head-on collision), where a = [(A-1)/(A+1)]2. This gives the maximum energy loss in a collision at E1 is (1-a)E1. The average loss is given by (1-a)E1/2.
The average cosine of the scattering angle (in the Laboratory system of coordinates), <cosy> = 2/3A, where A is nuclear mass in terms of neutron mass. For high A, <cosy> approaches zero, indicating a tendency to isotropy (i.e. all angles are equally probable).
The logarithmic energy decrement is given by log(E1 / E2). The average value of this quantity, per collision is given by x = 2/(A+2/3), which is independent of initial neutron energy. This indicates that, in every elastic collision, on an average, the neutron energy decrement is by a constant ratio, irrespective of its initial energy. From this, the number of collisions needed to bring a neutron from an initial energy E0 to a given energy E, is given by (1/x)ln(E0 / E). Thus the number of collisions required to slow down a 2 MeV neutron to 0.025 eV is given by ln(2´106/0.025) / x.
If E0 is an arbitrary high energy, the logarithmic decrement to a given energy E is ln(E0/E). Keeping the E0 as the reference (initial) energy, a quantity Lethargy can be defined as u = ln(E0/E). As E decreases u increases. Taking differentials, du = -dE/E. du represents infinitesimal log energy decrement.
For a good moderator high x, high scattering cross-section and low absorption cross-section are preferred, for obvious reasons. xSs is known as Slowing-down Power; and xSs /Sa is called the Moderating Ratio (MR). A material with high MR is preferable. The slowing down parameters of various nuclei are given below:
|
Material |
a |
x |
Collisions to thermalise |
MR |
|
H |
0.0 |
1.0 |
18 |
H2O = 72 |
|
D |
0.11 |
0.72 |
25 |
D2O = 12000 |
|
Be |
0.64 |
0.21 |
85 |
159 |
|
C |
0.72 |
0.16 |
115 |
170 |
|
O |
0.78 |
0.12 |
150 |
|
|
U-238 |
0.98 |
0.008 |
2172 |
|
Fissile, fertile and the concept of breeder reactors: A ‘fissile’ material is one which fissions with neutron of any energy. U-233, U-235, Pu-239, and Pu-241 are examples for fissile nuclides. A ‘fertile’ nuclide is one which leads to the production of a fissile nuclide, on absorption of a neutron. Th-232 and U-238 are well known fertile nuclides. It is seen from the detailed cross-section behaviour of these fertiles, that they support fission only with very fast neutrons, i.e. beyond about 1 MeV. At lower energies they have high potential of absorption of neutrons, and consequently converting to fissile nuclides. Such a conversion, wherein a nucleus, which is not ordinarily fissile, is converted to fissile is called breeding. Thus the concept of breeding is a concept of artificial production of fuel for nuclear reactors. This is explained further below:
The term ‘breeding’ refers to production of more fissile than consumed, in a reactor. Nuclear transmutations take place in a reactor due to continual nuclear interactions and radioactive decays, leading to the production of a variety of new nuclei, not present in the initial feed of materials in the reactor. Some of the newly produced nuclei are advantageous and some disadvantageous, but such new arrivals are inevitable. The new arrivals include new ‘fissile’ material and this becomes the most prominent among the materials newly produced in the transmutations. The initial feed of the fuel is made of the fissile material (U-235, U-233 or Pu-239) and the fertile material (U-238 or Th-232) in a calculated proportion. The following are the routes in which a fertile nucleus gets transmuted into a fissile nucleus:

In other words, a neutron capture in a fertile nuclide, followed by two successive b emissions, leads to the production of a fissile nuclide. The relevant half-lives of b emission are given in the brackets. U-238 is the fertile material used in most of the reactors and hence the fissile material Pu-239 is inevitably generated in each of them. It must be noted that the newly generated nuclei undergo all probable interactions and decays, so that they have both production and destruction routes. However, through a proper combination of fissile, fertile and other materials arranged in a carefully worked out geometry, together with proper reprocessing schemes, it is possible to realize a fissile production rate that exceeds the fissile consumption rate. A reactor system in which this has been realized is called a ‘breeder reactor’.
Conversion of fertile to fissile is possible over a wide energy range, but ‘adequate’ conversion is possible only in an appropriate range. In a reactor, the conversion depends on the available neutrons over and above what is required to sustain the fission chain and the inevitable losses due to leakage and unproductive absorptions. The parameter h governs conversion probability. h is basically defined for a fissioning nucleus, but could be derived also for a mixture of fissionable materials.
h = No. of neutrons produced (in fission) ¸ No. of neutrons absorbed
= nsf / (sf + sc) = n/(1+a), where
n = No. of neutrons produced per fission; a = sc/sf .
All the above parameters depend on neutron energy. n generally increases with energy. a and hence h show marked variation with fluctuations due to cross-section resonances. The figure below shows the energy dependence of h for the three fissile nuclides viz. U-235, Pu-239 & U-233.

h of the major fissile nuclides
If breeding (fissile production > fissile consumption) is desired then h must satisfy a minimum criterion, which could be logically derived as follows:
No. of neutrons absorbed by fissile = 1 (say)
No. of neutrons produced = h (by definition)
Out of h neutrons, one must be reserved to continue the fission chain in the fissile. Some L neutrons would be lost unproductively (due to parasitic capture and leakage). Hence the no. of neutrons available for capture by the fertile nucleus to do conversion is given by h - (1+L). Obviously this must be ³ 1. Thus,
h - (1+L) ³ 1 or h ³ 2 + L.
Hence the fissile material chosen and the energy spectrum of the neutrons must be such as to have h as much greater than 2 as possible. From the above, the ‘breeding ratio’ could be written as BR = h - (1+L), since this represents the number of neutrons absorbed in the fertile nucleus for every neutron absorbed in the fissile, assuming that the fertile absorption leads to conversion.
From the energy variation of h, the following are observed:
At energies close to thermal (0.025eV), only U-233 has h well above 2. At very high energies (>1 MeV), all the nuclides show marked increase in h. It is impractical to sustain neutron spectrum above 1 MeV, mainly due to inevitable energy degradation by inelastic scattering, and the fast spectrum is generally in the range 10 keV – 1 MeV, with its maximum around a few 100 keV. In this range, Pu-239 has h well above 2, and hence has become the undisputed fissile candidate for breeder reactors with fast neutrons.
The degree of conversion of fertile to fissile is given by the conversion ratio (CR), defined as
CR = Fissile mass produced = FP.
Fissile mass destroyed FD
CR is called breeding ratio (BR) if it exceeds unity indicating production in excess of consumption.
BR = FP > 1.
FD
The breeding gain G= BR-1, is given by
G = FG/FD
= Fissile gained / Fissile destroyed.
As most of the fissile absorption in the thermal reactor happens in the 0.01 to 1eV range, and in the fast reactor above 10 keV, the best fissile fuel is U-233 for a thermal reactor and Pu-239 for fast reactor with respect to breeding gain, based on the h values.